Python floor division is a powerful Python arithmetic operator that helps programmers divide numbers while discarding the remainder.
Unlike standard division, which returns a float, the Python // operator gives the largest whole number less than or equal to the actual result.
This makes it extremely useful in Python integer math, especially when you need clean, predictable results for loops, indexing, or Python dataset chunking.
Understanding integer division in Python is essential for beginners and advanced developers alike, as it forms the foundation for tasks like pagination, array indexing, and algorithm design.
Mastering floor division ensures accurate calculations across diverse Python applications.
How the Floor Division Operator (//) Works
The Python // operator calculates the integer quotient by dividing numbers and rounding down to the nearest whole number.
For positive numbers, it behaves similarly to truncation, but for negative numbers, it rounds toward negative infinity.
This is why understanding how Python handles negative division is critical when applying Python division rounding rules in your programs.
The operator works consistently across integers and floating-point numbers, making floor division with integers and floats versatile for multiple use cases.
For example, 7 // 2 results in 3, while -7 // 2 results in -4. This behavior illustrates truncation vs floor difference and emphasizes integer quotient calculation in Python.
Using the Python double slash operator allows programmers to safely perform Python remainder calculation and efficiently manage Python arithmetic operators when designing functions or algorithms.
Floor Division Syntax and Basic Usage
The syntax for it is simple: a // b. Here, a is the dividend and b is the divisor. The operator performs floor division with integers and floats, producing an integer if both operands are integers, or a float if one operand is a float.
For example, 10 // 3 yields 3, while 10.0 // 3 yields 3.0. Understanding how to use the double slash operator is key to safely performing Python integer rounding in loops, lists, or functions.
A comparison between floor vs truncation Python is helpful. While truncation just removes the decimal part, floor division for algorithm design ensures numbers round down.
The Python math.floor function can replicate // results for floats, reinforcing Python floor division vs math.floor.
Using this in basic operations also prepares you for performing chunk-based operations in Python.
Python Floor Division vs Regular Division (/)
Understanding true division vs floor division is important. Regular division / always returns a float, even for integers. For example, 7 / 2 gives 3.5, while 7 // 2 gives 3.
This difference highlights difference between / and // in Python and explains why safe integer division in Python often requires //.
Negative numbers demonstrate Python division rounding rules clearly. For instance, -7 / 2 gives -3.5, but -7 // 2 gives -4, showing how Python handles negative division.
Using // instead of / prevents unexpected decimal results and ensures your Python floor division use cases work correctly in indexing, Python dataset chunking, and loop calculations.
Floor Division with Negative Numbers
Negative number floor division behaves differently from positive numbers. Python rounds results toward negative infinity instead of truncating toward zero.
This is crucial when applying this edge cases in algorithms or data calculations. For example, -10 // 3 results in -4, not -3.
Understanding how Python handles remainder and quotient is essential here. Using the Python modulo operator alongside // ensures the formula division equation N = D(N//D) + (N % D)* holds true, even for negative dividends or divisors.
This is particularly useful in Python binary search midpoint calculations and safe integer division in Python scenarios.
Type Behavior in Floor Division
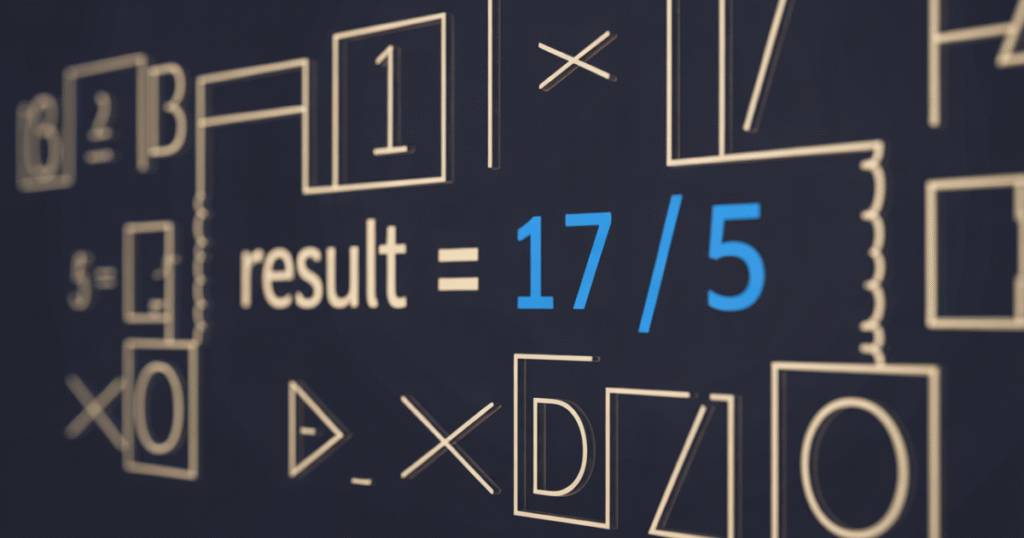
The type behavior of floor division in Python depends on the operands. Two integers return an integer, but mixing a float produces a float.
For example, 9 // 2 gives 4, but 9.0 // 2 gives 4.0. Understanding this is crucial for Python division behavior in functions and large calculations.
The Python math.floor function can be used with floats to match // results. This is a reliable alternative when working with mixed data types.
Understanding floor of real numbers ensures consistent results in Python integer math and Python sequence operations across different numeric types.
Floor Division with NumPy Arrays
Working with floor division in NumPy allows element-wise calculations across arrays efficiently.
Using NumPy floor division with the // operator applies element-wise floor division across arrays or matrices.For example, np.array([10, 20, 30]) // 7 results in [1, 2, 4].
This method is widely used in Python array indexing and Python dataset chunking.
It ensures computations remain fast and accurate while handling large datasets, and is more efficient than looping through elements manually.
Using Floor Division in Loops and Iterations
Python loops using floor division are common for splitting sequences or calculating midpoints. The // operator helps in using floor division in loops and indexing, ensuring integers for range calculations.
For instance, in a binary search, (left + right) // 2 safely gives a midpoint without floating-point errors.
It is also practical for performing chunk-based operations in Python within loops.
Dividing a list into equal segments can be done by calculating len(list) // n, ensuring each loop iteration handles the correct subset of elements efficiently.
Floor Division in List Indexing and Slicing
Python list splitting relies on calculating middle index using floor division. For example, mid = len(names) // 2 returns the middle index of a list, even if its length is odd.
This is essential for Python sequence operations where indexes must be integers.
Slicing lists with // ensures Python dataset chunking is clean and precise.
Whether splitting a list for pagination or iterating in loops, using floor division in loops and indexing prevents off-by-one errors and guarantees consistent results.
Real-World Applications of Floor Division
Its use cases include Python chunking and pagination, converting time units, or evenly distributing items.
For example, in Python pagination logic example, calculating pages from total_items // items_per_page ensures integer results.
It is also practical for splitting datasets into equal parts in Python or performing integer quotient calculation in Python for allocation problems.
Its predictable behavior makes it reliable in financial calculations, grid layouts, and algorithm design.
Floor Division in Functions and Algorithms
Floor division for algorithm design ensures that divisions remain precise and integers are returned.
It is useful in Python floor division examples within functions to divide data, calculate middle points, or handle repeated operations.
Algorithms like binary search, chunk processing, and array manipulation benefit from safe integer division in Python.
Using Python floor division use cases in function design ensures stability and avoids floating-point inaccuracies in larger computations.
Advanced Techniques Using Floor Division

Advanced techniques involve nested operations, combining Python // operator with Python modulo operator to get both quotient and remainder.
This is ideal for floor division for algorithm design and Python integer math optimizations.
It is also applied in multi-step calculations, performing chunk-based operations in Python, and iterative processes where precise indexing or segmentation is needed.
This in Python provides predictable, robust results in complex scenarios.
Common Mistakes and Pitfalls to Avoid
A common mistake is assuming truncation equals floor. Another is mishandling negative number floor division or mixing ints and floats without understanding Python division behavior.
These can lead to its edge cases.
Always remember the formula division equation N = D(N//D) + (N % D)*. Misapplying it can produce wrong indexes, midpoints, or chunk calculations.
Careful use of Python remainder calculation ensures accurate outputs in loops, lists, and functions.
Debugging and Testing Floor Division Code
Debugging requires checking results against known examples. Use small test cases to verify Python floor division examples and how Python handles remainder and quotient.
Unit tests can validate type behavior of floor division in Python and ensure consistency with Python floor division vs math.floor.
This step prevents errors in loops, indexing, and chunk-based computations.
Alternatives to Floor Division in Python

The Python math.floor function can replace // when working with floats. Casting to int is another alternative, but it only truncates, highlighting the truncation vs floor difference.
Choosing the right alternative depends on your goal. For precise integer division, Python floor division vs math.floor ensures predictable results.
For simpler approximations, truncation may suffice, but it does not match the safety of // in safe integer division in Python.
Summary and Final Thoughts
Python Floor Division is a powerful tool for integer calculations, loops, indexing, and algorithms.
Understanding when to use floor division in Python, Python floor division use cases, and Python floor division edge cases ensures you write accurate and efficient code.
Using how to use the double slash operator correctly allows you to handle floor division with integers and floats, perform Python chunking and pagination, calculate midpoints, and design stable algorithms.
Mastering floor division elevates your Python coding skills and prevents subtle arithmetic errors.
FAQs
What is 7 floor division 2?
7 floor division 2 (7 // 2) in Python equals 3, as it returns the largest integer not exceeding the result.
What is the floor division of 5 2 in Python?
The floor division of 5 // 2 in Python is 2.
Is floor division efficient in Python?
Yes, floor division is efficient in Python, especially for integer calculations, loops, and indexing.
Is floor division different in Python 2?
Yes, in Python 2, floor division with integers behaves differently: 5 / 2 returns 2 instead of a float.
How to code floor division in Python?
Use the double slash operator (//), e.g., result = 5 // 2, to perform floor division.